Постановка задачи
Можно ли поставить на пустой шахматной доске восемь ферзей так, чтобы ни один из них не «атаковал» другого, то есть никакие два ферзя не стояли бы на одном и том же столбце или на одной и той же строке или на одной и той же диагонали? Требуется определить максимально возможное число расстановок 8 ферзей в соответствии с указанными правилами и вывести все допустимые варианты расстановок.
В старых книгах про головоломки и математическую смекалку вы сможете найти эмпирические алгоритмы решения подобных задач, которые существенно снижают число проверяемых расстановок. Однако если вы нашли одно или несколько решений этими способами, то вопрос о наличии других возможных решений остается открытым.
Гарантированный ответ может дать только полный перебор возможных вариантов расстановки, который без учета всех ограничений задает число вариантов 88 = 224= 16 777 216 (Вариант 1).
Генерация расстановок, когда следующий (по номеру вертикали-столбца) ферзь ставится на горизонталь-строку с учетом несовпадения номера строки со всеми предыдущими, уменьшает число вариантов до 8! =40320 (Вариант 2).
Рассмотрим задачу полного перебора расстановок и оценим эффективность его по времени решения.
Алгоритм решения
Если у нас есть некоторая расстановка восьми ферзей, то количество попарных проверок положений ферзей равно сумме чисел от 7 до 1 с шагом 1, то есть равно 28. Действительно, число проверок положения первого ферзя со всеми остальными равна 7, второго со всеми остальными кроме первого равна 6 (если 1-й ферзь не атакует 2-го, то это означает, что и 2-й ферзь не атакует 1-го — свойство коммутативности). И так далее, последняя проверка — положение 7-го и 8-го ферзей.
Создадим массив из девяти чисел p[9]. Индекс элемента от 1 до 8 будет соответствовать букве (номеру) вертикали-столбца, а значение элемента — номеру строки-горизонтали, где размещается один из 8 ферзей.
Элемент p[0] будем использовать как счетчик количества «непересечений» всех восьми ферзей при заданной расстановке. Если это число будет равно 28, то тогда такая расстановка дает ответ на поставленный вопрос.
Например:
{5,8,4,1,7,2,6,3} => 28 непересечений;
{2,5,7,1,3,8,6,4} => 28 непересечений;
{2,4,7,1,3,8,6,5} => 25 непересечений;
{2,4,6,8,1,3,5,7} => 25 непересечений;
{2,3,4,5,6,7,8,1} => 6 неперсечений.
Для генерации расстановок выберем первый вариант (полный перебор), требующий проверки 16777216 вариантов.
Введем подсчет времени решения задачи с помощью метода TimePoisk(), уже использованного в задаче «Простые числа». Если окажется, что время на полный перебор достаточно велико, то перейдем к генерации расстановок по второму способу (алгоритмически он кажется чуть более сложным).
Программная реализация
Создадим класс F8 («восемь ферзей») с полями:
public byte[] p = new byte[9]; — рассмотренный выше массив;
public DateTime tstart, tfinish; — временные метки начала и конца поиска;
и методами:
public void provP() — проверка одной расстановки;
public bool provG() — проверка нахождения ферзей (хотя бы одного) на главных диагоналях: нет — true, есть — false
public void provM() — перебор 16 777 216 вариантов и проверка каждого из них с помощью метода provP(); Для полного перебора пришлось написать восемь вложенных циклов.
public void TimePoisk() — расчет интервал времени между tstart и tfinish.
Вариант программы представлен ниже:
using System;
namespace ВосемьФерзей
{
class Program
{
static void Main(string[] args)
{
F8 d = new F8();
d.tstart = DateTime.Now;
d.provM();
d.tfinish = DateTime.Now;
d.TimePoisk();
Console.ReadKey();
}
}
class F8
{
public DateTime tstart, tfinish; // время старта и финиша решения задачи
public byte[] p = new byte[9];
// p[0] - счетчик пересечений в расстановке
// p[1] - номер горизонтали на вертикали a. Если p[1]=5, то это клетка а5
// p[2] - номер горизонтали на вертикали b. Если p[1]=8, то это клетка b8
// ...
// p[8] - номер горизонтали на вертикали h. Если p[1]=3, то это клетка h3
// Примеры:
// {0,5,8,4,1,7,2,6,3}; = 28 непересечений
// {0,2,5,7,1,3,8,6,4}; = 28
// {0,2,4,7,1,3,8,6,5}; = 25 неперсечений
// {0,2,4,6,8,1,3,5,7}; = 25
// {0,2,3,4,5,6,7,8,1}; = 6 неперсечений
// Необходима проверка 28 пар точек: 7 (1-я с остальными) +
// 6 (2-я с остальными) + ... + 1 (7-я с 8-й) = 28
// Проверка 28 пар клеток с координатами:
// (p[j1],j1) и (p[j2],j2) - (строка, столбец)
public void provP()
{
bool b1, b2, b3;
for (byte j1 = 1; j1 < 8; j1++)
for (byte j2 = (byte)(j1 + 1); j2 <= 8; j2++)
{
b1 = (p[j1] != p[j2]); // не на одной горизонтали (строке)
b2 = (p[j2] - p[j1]) != (j2 - j1); // не на одной диагонали (45 град)
b3 = (p[j1] + j1) != (p[j2] + j2); // не на одной диагонали (135 град)
if (b1 && b2 && b3)
p[0]++; // если не бьют друг друга
}
}
// Проверка нахождения ферзей (хотя бы одного)
// на главных диагоналях: нет - true, есть - false
public bool provG()
{
bool b = false;
for (int i = 1; i <= 8; i++)
{
if ((i == p[i]) | ((i + p[i]) == 9))
{
b = true;
}
if (b)
break; // выход из цикла
}
return b;
}
// Перебор 8^8 = 16 777 216 вариантов
public void provM()
{
int count = 0; // счетчик допустимых расстановок
// byte j1 = 2; // если первого ферзя поставить на a2,
// а заголовок цикла закомментировать
for (byte j1 = 1; j1 <= 8; j1++)
{
p[1] = j1;
for (byte j2 = 1; j2 <= 8; j2++)
{
p[2] = j2;
for (byte j3 = 1; j3 <= 8; j3++)
{
p[3] = j3;
for (byte j4 = 1; j4 <= 8; j4++)
{
p[4] = j4;
for (byte j5 = 1; j5 <= 8; j5++)
{
p[5] = j5;
for (byte j6 = 1; j6 <= 8; j6++)
{
p[6] = j6;
for (byte j7 = 1; j7 <= 8; j7++)
{
p[7] = j7;
for (byte j8 = 1; j8 <= 8; j8++)
{
p[8] = j8;
p[0] = 0; // счетчик обнулим
provP();
if (p[0] == 28)
{
bool b = provG(); // true - если хотя бы один ферзь на главных диагоналях
b = false; //- тогда все 92 решения. Если закомментируем его, то 12
if (!b)
{
count++;
Console.Write("{0}): ", count);
for (int i = 1; i <= 8; i++)
Console.Write(" {0} ", p[i]);
Console.WriteLine();
}
}
} // конец цикла по j8
} } } } } } }
Console.WriteLine("Всего расстановок - {0}", count);
}
// Интервал времени между tstart и tfinish
public void TimePoisk()
{
int dt, ds, dm, dh;
dt = tfinish.Hour * 3600 + tfinish.Minute * 60 + tfinish.Second - tstart.Hour * 3600 - tstart.Minute * 60 - tstart.Second;
dh = dt / 3600;
dm = (dt - dh * 3600) / 60;
ds = (dt - dh * 3600 - dm * 60);
if (dt < 60)
Console.WriteLine("Время поиска: секунд - {0}", ds);
else if (dt < 3600)
Console.WriteLine("Время поиска: минут - {0}, секунд - {1}", dm, ds);
else
Console.WriteLine("Время поиска: часов - {0}, минут - {1}, секунд - {2}", dh, dm, ds);
}
}
}
Результат

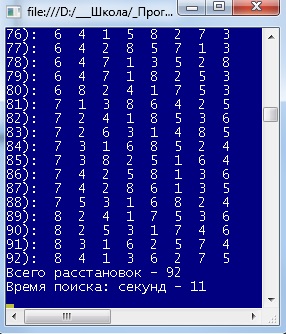
Здесь приведены начало и конец всего решения.
Обсуждение и задания для самостоятельной работы
Время поиска вариантов (11 секунд) вполне приемлемое. Запрограммируйте 2 вариант генерации расстановок и сравните время выполнения программы с первым вариантом.
Заметим, что возможны всего 92 расстановки. Запретив размещение ферзей на главных диагоналях, для чего просто закомментируйте оператор в теле циклов:
b = false; //- тогда все 92 решения. Если закомментируем его, то 12,
и вы получите действительно только 12 допустимых решений.
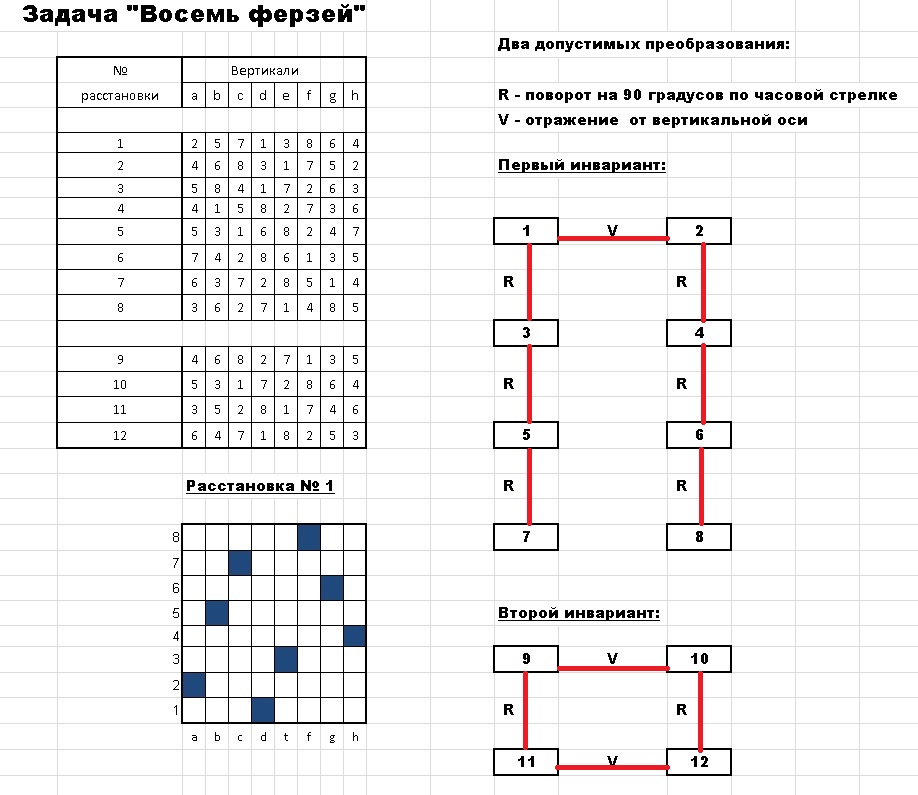
Подумайте, сколько можно получить решений из одного допустимого, если выполнить повороты доски на 90, 180 и 270 градусов, а также зеркальные отражения относительно осей симметрии. Запишите ваши решения в комментарии к статье, они будут опубликованы.
Перейдите к задачам для самостоятельного решения.
NEW: Наш Чат, в котором вы можете обсудить любые вопросы, идеи, поделиться опытом или связаться с администраторами.

|

|

|

|
Спасибо, всё очень понятно.