Содержание
1. Постановка задачи
2. Алгоритм Б
3. Программная реализация
1. Постановка задачи
(дословное воспроизведение задания)
Дан список точек плоскости с целочисленными координатами. Необходимо определить:
1) номер координатной четверти K, в которой находится больше всего точек;
2) точку A в этой четверти, наименее удалённую от осей координат;
3) расстояние R от этой точки до ближайшей оси.
Если в нескольких четвертях расположено одинаковое количество точек, следует выбрать ту четверть, в которой величина R меньше.
При равенстве и количества точек, и величины R необходимо выбрать четверть с меньшим номером K.
Если в выбранной четверти несколько точек находятся на одинаковом минимальном расстоянии от осей координат, нужно выбрать первую по списку.
Точки, хотя бы одна из координат которых равна нулю, считаются не принадлежащими ни одной четверти и не рассматриваются.
Напишите эффективную, в том числе по памяти, программу, которая будет решать эту задачу.
Перед текстом программы кратко опишите алгоритм решения задачи и укажите используемый язык программирования и его версию.
Описание входных данных:
В первой строке вводится одно целое положительное число — количество точек N.
Каждая из следующих N строк содержит координаты очередной точки — два целых числа (первое — координата x, второе — координата у).
Описание выходных данных:
Программа должна вывести номер выбранной четверти K, количество точек в ней M, координаты выбранной точки A и минимальное расстояние R по образцу, приведённому ниже в примере.
Пример входных данных:
7
−3 4
1 2
1 1
0 4
−2 −3
−6 8
−12 1
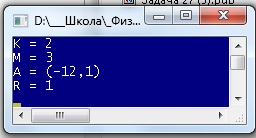
Пример выходных данных для приведённого выше примера входных данных:
K = 2
M = 3
A = (−12, 1)
R = 1
Примечание.
Считайте, что во входных данных имеется хотя бы одна точка, не лежащая на осях координат.
2. Алгоритм Б
Эффективная по памяти программа не должна использовать массив координат всех точек. Если мы будем последовательно анализировать координаты каждой новой точки, то очевидно, что достаточно подсчитывать число точек в каждой координатной четверти (квадранте) — массив M[ ], вычислять и заносить минимальное расстояние в массив R[ ], также как и координаты (x, y) в массивы xA[ ] и yA[ ], то после обработки последней точки несложно получить требуемые результаты. Алгоритм A писать для этой задачи не целесообразно.
3. Программная реализация
using System;
using System.IO;
namespace Задача_27_3_
{
class Program
{
static void Main(string[] args)
{
int N, x, y;
string data = "data.txt";
StreamReader sr = new StreamReader(data);
int[] M = new int[4]; // число точек в каждом квадранте
int[] R = new int[4]; // минимальное расстояние до оси
int[] xA = new int[4]; // координаты искомых точек
int[] yA = new int[4];
for (int i = 0; i < 4; i++)
{
M[i] = 0;
R[i] = 0;
}
int k;
N = Convert.ToInt32(sr.ReadLine());
for (int i = 0; i < N; i++)
{
// извлечение координат очередной точки
string xy = sr.ReadLine();
int z = xy.IndexOf(' ');
x = Convert.ToInt32(xy.Substring(0, z));
y = Convert.ToInt32(xy.Substring(z + 1));
// номер квадранта
k = 0; // если лежит на оси х или у
if (x > 0 & y > 0)
k = 1;
if (x < 0 & y > 0)
k = 2;
if (x < 0 & y < 0)
k = 3;
if (x > 0 & y < 0)
k = 4;
// анализ расстояния
if (k > 0)
{
M[k - 1]++;
if ((Math.Min(Math.Abs(x), Math.Abs(y)) < R[k - 1]) | R[k - 1] == 0)
{
R[k - 1] = Math.Min(Math.Abs(x), Math.Abs(y));
xA[k - 1] = x;
yA[k - 1] = y;
}
}
}
// Точка с минимальным расстоянием
k = 0;
for (int i = 1; i < 4; i++)
if ((M[i] > M[k]) | ((M[i] == M[k]) & (R[i] < R[k])))
k = i;
// Результаты
Console.WriteLine("K = {0}", k+1);
Console.WriteLine("M = {0}", M[k]);
Console.WriteLine("A = ({0},{1})", xA[k], yA[k]);
Console.WriteLine("R = {0}", R[k]);
Console.ReadKey();
}
}
}
Пример решения для заданных исходных данных:
NEW: Наш Чат, в котором вы можете обсудить любые вопросы, идеи, поделиться опытом или связаться с администраторами.

|

|

|

|