Впервые кривые были представлены в 1962 году французским инженером Пьером Безье (Рено), который, разработав независимо от де Кастельжо (Ситроен), использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых. Впоследствии это открытие стало одним из полезных инструментов компьютерной графики.
Четыре опорные точки P0 (start), P1(control1), P2(control2) и P3(finish), заданные в 2-мерном пространстве, определяют форму кривой.
Методы класса Graphics DrawBezier( ) и DrawBeziers( ) позволяют непосредственно построить на плоскости 0xy любую кривую Безье. Однако иногда бывает полезно иметь и параметрическое представление кривой.
Постановка задачи
- Заданы 4 опорные точки кривой Безье. Требуется реализовать метод де Кастельжо для понимания способа построения кривой. Параметрически кривая Безье задается в виде:
- . (1)
Решение
Любая точка x(t) на отрезке [x1, x2] параметрически задается уравнением:
x(t) = (1-t) x1 + t x2 , (2)
где t изменяется в интервале [0, 1].
Алгоритм:
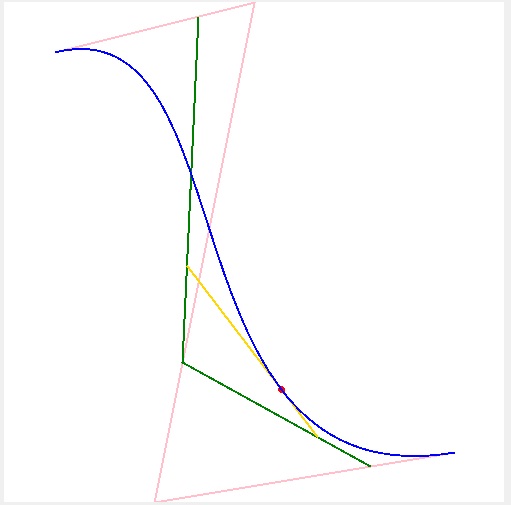
1) Точки 0, 1, 2, 3 (нулевой уровень) по порядку соединяются отрезками: 0 → 1, 1 → 2, 2 → 3. Получаются три отрезка.
2) На отрезках берутся точки 0, 1, 2 (первый уровень), соответствующие текущему t по формуле (2), соединяются между собой. Получается два отрезка.
3) На этих отрезках берутся точки (0, 1) (второй уровень), соответствующие текущему t по формуле (2), соединяются. Получается один отрезок.
4) На отрезке берётся точка 0, соответствующая текущему t по формуле (2).
5) При запуске примера — она красная. Совокупность этих точек описывает кривую Безье.
Для каждого t из интервала от 0 до 1 по этому правилу, соединяя точки на соответствующем расстоянии, из 4 отрезков делается 3, затем из 3 так же делается 2, затем из 2 отрезков – точка, описывающая кривую для данного значения t.
Этот алгоритм рекурсивен, назовем метод для получения координат точек PointF CastR(p, t, n, m), где p — массив исходных точек, t — параметр, n — номер уровня (0, 1, 2, 3), m — номер точки на этом уровне. Тогда p[m] = CastR(p, t, 0, m) ], а CastR(p, t, 3, 0) — искомая точка на кривой Безье. Для нахождения промежуточной точки на отрезке создадим метод PointF Lin1(PointF, PointF, t).
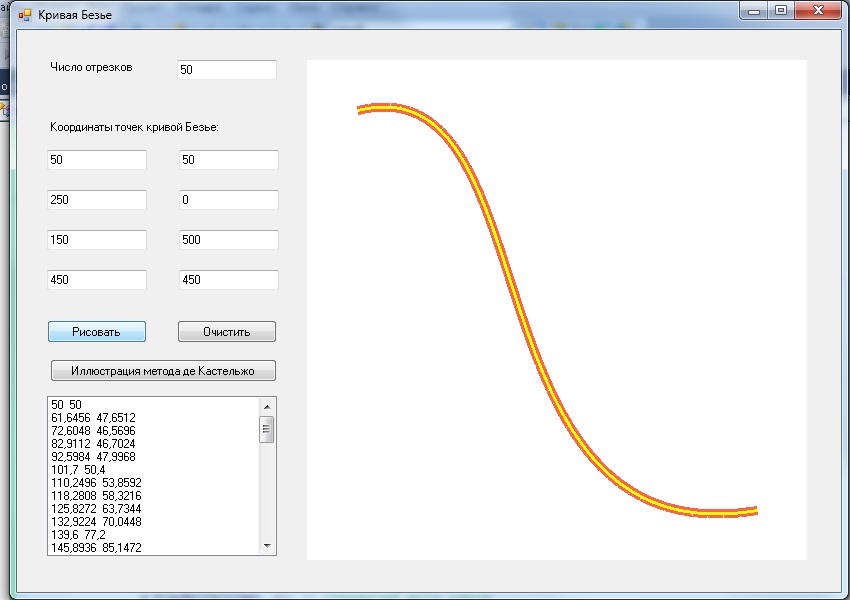
Исходная форма приложения представлена ниже:
Добавим также невизуальный элемент timer1. Окно внизу слева (listBox1) будем использовать для вывода координат точек кривой Безье, а квадрат справа (pictureBox1) для вывода кривой Безье и иллюстрации метода де Кастельжо.
Текст файла Form1.cs :
using System;
using System.Drawing;
using System.Windows.Forms;
namespace Безье1
{
public partial class Form1 : Form
{
Point[] p = new Point[4]; // опорные точки
Graphics g; // графический контент - холст
double tim = 0.0; // параметр кривой [0,1]
// точка на отрезке (р1,р2) от t
PointF Lin1(PointF p1, PointF p2, double t)
{
PointF q = new PointF();
q.X = Convert.ToSingle(p2.X * t + p1.X * (1 - t));
q.Y = Convert.ToSingle(p2.Y * t + p1.Y * (1 - t));
return q;
}
// метод де Кастельжо (с рекурсией)
PointF CastR(Point[] p, double t, int n, int m)
{
if (n == 0)
return p[m];
else
return Lin1(CastR(p, t, n - 1, m), CastR(p, t, n - 1, m + 1), t);
}
// конструктор класса
public Form1()
{
InitializeComponent();
g = this.pictureBox1.CreateGraphics(); // холст
// перенос опорных точек в массив
p[0].X = Convert.ToInt32(textBox1.Text);
p[0].Y = Convert.ToInt32(textBox2.Text);
p[1].X = Convert.ToInt32(textBox3.Text);
p[1].Y = Convert.ToInt32(textBox4.Text);
p[2].X = Convert.ToInt32(textBox5.Text);
p[2].Y = Convert.ToInt32(textBox6.Text);
p[3].X = Convert.ToInt32(textBox7.Text);
p[3].Y = Convert.ToInt32(textBox8.Text);
timer1.Stop();
}
private void button1_Click(object sender, EventArgs e)
{
// расчет точек кривой
int N = Convert.ToInt32(textBox9.Text); //число
double d = 1.0 / N; // шаг delta t
double t = 0.0; // параметр t
PointF q = new PointF(); // следующая точка
PointF r = CastR(p, t, 3, 0); // начальная точка
listBox1.Items.Clear(); // очистка списка для точек
listBox1.Items.Add(r.X.ToString() + " " + r.Y.ToString());
Pen pen = new Pen(Color.Tomato, 9); // перо
// вывод точек в список и рисование кривой
for (int i = 0; i < N; i++)
{
t += d;
q = CastR(p, t, 3, 0); // следующая точка
listBox1.Items.Add(q.X.ToString() + " " + q.Y.ToString());
g.DrawLine(pen, r, q);
r = q;
}
// проверка через метод из Graphics
pen = new Pen(Color.Yellow, 3); // перо
g.DrawBeziers(pen, p); // стандартный метод класса
}
// очистка и остановка
private void button2_Click(object sender, EventArgs e)
{
g.Clear(Color.White);
timer1.Stop();
}
// Старт иллюстрации метода де Кастельжо
private void button3_Click(object sender, EventArgs e)
{
// timer1.Tick=40 мс
timer1.Start();
}
// Иллюстрация метода де Кастельжо
private void timer1_Tick(object sender, EventArgs e)
{
Pen pen = new Pen(Color.White);
if (tim > 1.0)
tim = 0.0;
else
{
g.Clear(Color.White);
pen.Width = 2;
// соединяем исходные точки (3 отрезка)
pen.Color = Color.Pink;
g.DrawLines(pen, p);
// два отрезка
pen.Color = Color.Green;
g.DrawLine(pen, CastR(p, tim, 1, 0), CastR(p, tim, 1, 1));
g.DrawLine(pen, CastR(p, tim, 1, 1), CastR(p, tim, 1, 2));
// один отрезок
pen.Color = Color.Gold;
g.DrawLine(pen, CastR(p, tim, 2, 0), CastR(p, tim, 2, 1));
SolidBrush br = new SolidBrush(Color.Red);
// искомая точка
PointF qR = CastR(p, tim, 3, 0);
g.FillEllipse(br, qR.X - 3, qR.Y - 3, 7, 7);
// вся кривая
pen.Color = Color.Blue;
g.DrawBeziers(pen, p); // стандартный метод класса
// изменение параметра
tim += 0.0025;
}
}
}
}
Результат построения кривой Безье:
И иллюстрация метода де Кастельжо (t=0.75):
Предлагаю решить следующую задачу.
При перемещении движка слева направо лыжник скатывается по трамплину, заданному кривой Безье. Лучшие результаты будут размещены на нашем сайте.
NEW: Наш Чат, в котором вы можете обсудить любые вопросы, идеи, поделиться опытом или связаться с администраторами.

|

|

|

|
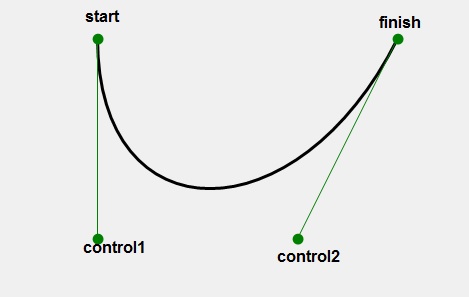
![{\mathbf {B}}(t)=(1-t)^{3}{\mathbf {P}}_{0}+3t(1-t)^{2}{\mathbf {P}}_{1}+3t^{2}(1-t){\mathbf {P}}_{2}+t^{3}{\mathbf {P}}_{3},\quad t\in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/26ff769812d3f7ad991b184a4ff63bfd08fd2919)

Понятно Вячеслав. Халява не проходит. Придется по данной блок-схеме писать программный код. Спасибо за оперативность.
Здравствуйте. Необходимо реализовать процесс построения кривой Безье по методу который содержиться по ссылке http://www.mathros.net.ua/kryvi-bezje.html. Скажите пожалуйста Ваш программный код реализует именно этот метод ци нет? Возможно мой вопрос несколько странный , однако, исходя из того, что в программировании я не силен прошу помочь. Спасибо.
Олег! Если сравнивать вторую часть Вашей статьи и мой алгоритм (построение одной кривой), то нет. Мой (рекурсивный) ближе к реальным алгоритмам компьютерной графики. Сшивка нескольких кривых в одну будет зависеть от типов промежуточных вершин.